Background
The Sabatier principle is at the core of our understanding of heterogeneous catalysis. Originally proposed around 1911 by the French chemist Paul Sabatier, this principle states that a good catalyst must bind the reactant at a strength which is "just right". If the binding is too weak, there is insufficient interaction to promote the reaction, whereas if the interaction is too strong, the reactant cannot desorb from the catalyst, leading to low amounts of the final product. Although this principle was originally an empirical one, the advancement of DFT and other in-silico techniques have allowed the Sabatier principle to be used as a quantitative basis to search for new catalysts. Many recent studies using machine learning and neural networks are also using the Sabatier principle as the conceptual basis for materials screening.
However, the Sabatier principle is thermodynamic in nature, and cannot predict how fast a reaction will occur. Instead, the binding energy and the corresponding thermodynamic landscape are used to estimate the true activity (rate laws). For this reason, a conceptual expansion is necessary to predict and rationalize the behavior of catalysts under real, non-equilibrium conditions. Currently, I am collaborating with experimentalists to expand the theory of electrocatalysis.
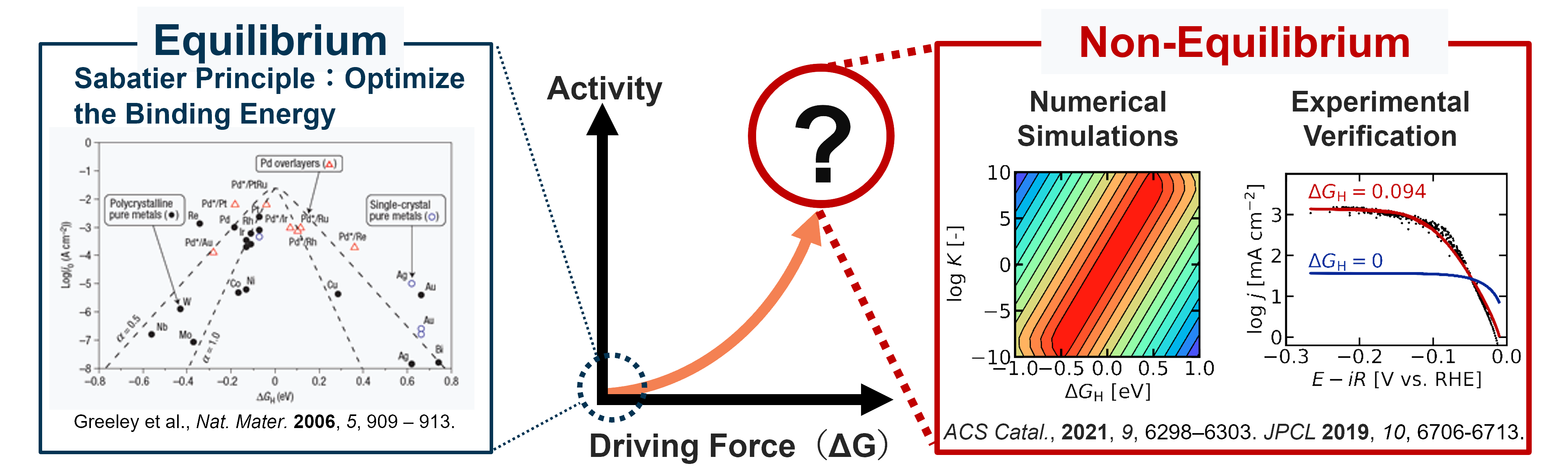
Comparison between existing catalyst theory (left) and my ongoing research (right)
Model Networks
Electrocatalysis
In electrocatalysis, there are several established mechanisms such as for the hydrogen evolution reaction (HER). So far, I have shown that the optimum binding energy can shift at higher rates of catalysis mathematically (2019 JPCL) and have shown experimentally that Pt, which is one of the best catalysts for the hydrogen evolution reaction, can be understood within this framework (2021 ACS Catal.). In this paper, I made a custom machine learning algorithm to compare experimental data with theoretical predictions, and to see how reliable the obtained fitting parameters are in a computationally efficient manner. I am working to expand this approach towards more complex mechanisms, such as oxygen evolution reaction (OER) so that we can rationalize the activity more accurately.
Selected Publications: JPCL 2024, ACS Catalysis 2021, JPCL 2019.
Michaelis-Menten Enzymes
Enzymes are a subclass of catalysts, and therefore, the mathematical models are quite similar to the modelling of electrocatalysts. In particular, Michaelis-Menten type enzymes have only a single intermediate and therefore, their reaction mechanism and the corresponding rate equation is almost identical to the HER. Based on this insight, I have proposed that the Michaelis-Menten constant Km, which is a measure of the binding affinity, should be equal to the substrate concentration for maximium activity. My bioinformatic analysis on a dataset of 1000 wild-type enzymes have Km values close to the substrate concentration, suggesting that even nature seems to respect the principle Km = [S] (2023 Nat. Commun.).
I am currently working with experimental biologists to verify the applicability of this principle. Once the behavior of each enzyme can be rationalized in relation to physicochemical parameters, I am hoping to expand the analysis from single enzymes to a network, which may lead to a general design principle of biological metabolism.
Selected Publications: Nat. Commun. 2023, Angewandte 2024
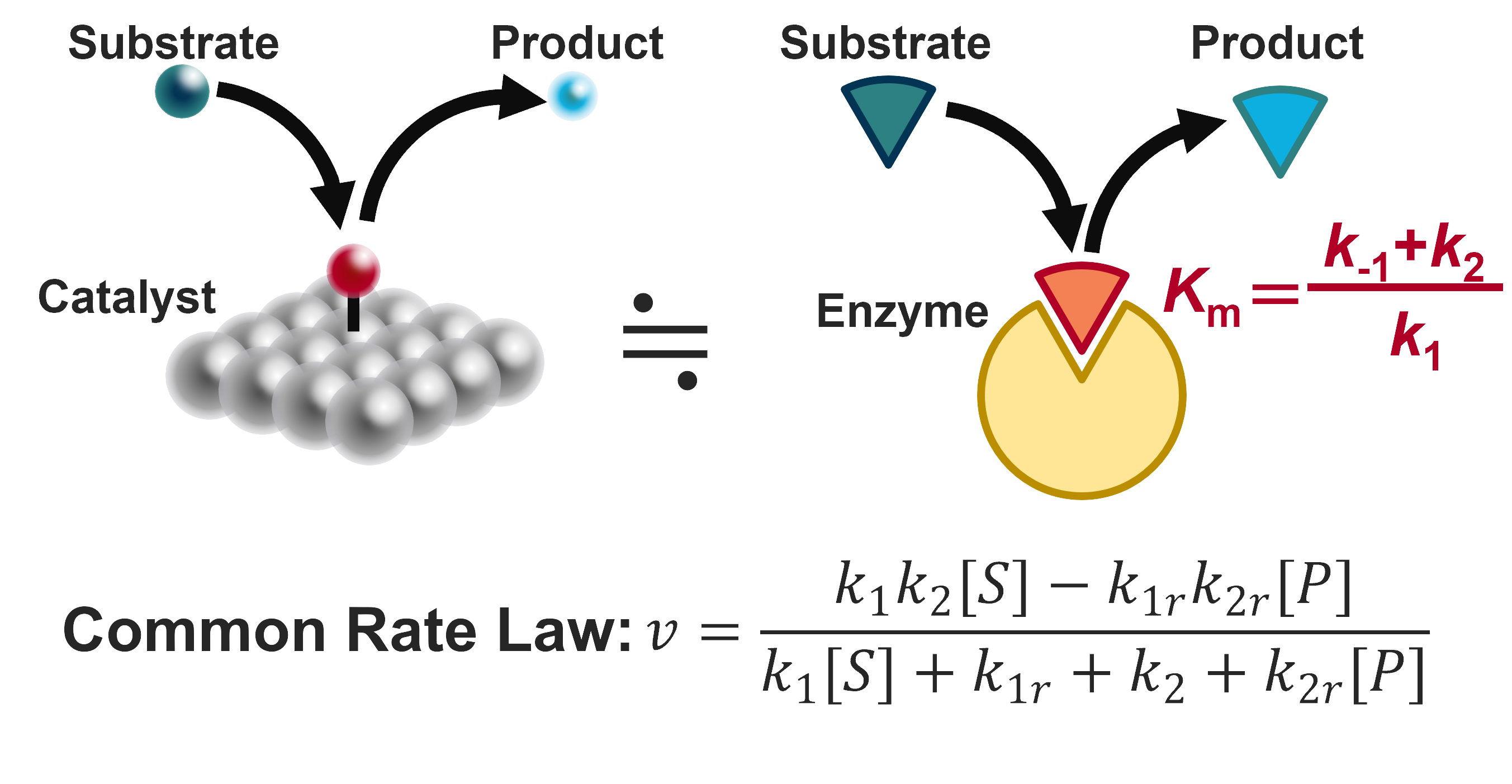
Similarity between catalysts and enzymes.
General Networks
Using model networks is the established approach in chemistry and microkinetics. However, this approach means every mechanism must be analyzed one-by-one. Furthermore, when the mechanism assumed initially becomes invalid, for example based on the detection of new intermediates using in-situ spectroscopy, the mathematical analysis must be performed again. To overcome this limitation, I am trying to make a quantitative theory which can predict the longterm behavior of multiple reaction mechanisms. My 2024 JPCL paper which attempts to rationalize the lifetime of catalysts with an unknown number (N) of intermediate species is one example of this approach.
Selected Publications: JPCL 2024